Pour investir dans l’immobilier locatif, le recours à l’emprunt est souvent obligatoire. Les sommes à investir sont importantes. Est-il possible d’investir dans du locatif sans apport ? Acheter pour louer sans apport de départ va-t-il bloquer tes projets ? Peut-on obtenir un prêt pour un investissement locatif sans apport et/ou sans CDI ?
Nous allons faire le tour de ces questions dans cet article.
Première bonne nouvelle, faire un investissement locatif sans apport est parfaitement possible. Je l’ai fait à plusieurs reprises comme tu pourras le lire. Beaucoup d’investisseurs immobiliers peuvent obtenir des prêts immobiliers sans apport pour les investissements locatifs.
Ce guide va t’aider à investir dans l’immobilier avec peu ou pas d’apport. Nous verrons qu’il est beaucoup plus difficile de faire de l’investissement locatif sans revenu et/ou sans CDI. Il ne faut pas confondre les deux. La banque fera très bien la différence !
Ensuite, je te donnerai ma méthode pour calibrer ton investissement locatif si tu veux emprunter sans apport. Tu verras aussi les 4 raisons qui sont intéressantes pour investir dans le locatif à crédit. Enfin, je t’expliquerai comment fonctionnent les mensualités et les intérêts dans les crédits immobiliers.
Tu peux aussi lire cet article où tu verras s’il vaut mieux investir cash ou crédit dans une place de parking ou tout autre investissement locatif.
Voici le sommaire de l’article :
- Investissement locatif sans apport ou sans argent : quelles différences ?
- La méthode pour trouver un prêt immobilier locatif sans apport
- Peut-on acheter de l’immobilier locatif sans CDI et sans apport ?
- Peut-on acheter des investissements locatifs parking sans apport ?
- 4 raisons de réaliser des investissements locatifs à crédit
- Comprendre le calcul des intérêts d’emprunt pour un achat immobilier locatif
Investissement locatif sans apport ou sans argent : quelles différences ?
Investir dans l’immobilier locatif sans apport
Investir dans l’immobilier locatif sans apport est faisable. En 2018, les taux sont très bas, les banques ont ouvert les vannes du crédit pour l’immobilier. Beaucoup d’investisseurs peuvent investir dans le locatif sans apport.
Réaliser un investissement locatif sans apport veut dire que la banque te prête de tout l’argent dont tu as besoin pour acheter un appartement, une maison ou un immeuble pour les louer sans faire d’apport.
Tu as besoin de 200000 € pour acheter un immeuble de rapport. Tu ne souhaites pas ou ne peux pas faire d’apport. La banque va alors te prêter les 200000 € pour que tu investisses dans l’immeuble de rapport sans apport. Tu peux donc acheter plusieurs appartement d’un seul coup sans apport.
L’argent sur tes comptes épargne n’est pas utilisé pour cet investissement locatif. Il est même possible que l’emprunteur n’a pas d’argent épargné. Dans certains cas, les banques pourront malgré tout financer le projet.
Comment obtenir un prêt immobilier sans argent ?
Obtenir un crédit immobilier sans argent ou sans revenu est beaucoup plus difficile que de trouver un prêt immobilier sans apport.
En 2013, j’ai visité une douzaine de banque pour trouver un prêt immobilier pour un investissement locatif de 50 garages. L’investissement total est de 90000 €, le rendement est proche de 15 % brut.
Je viens de quitter Leroy Merlin de mon plein gré avec un licenciement à l’amiable. Il me reste un an de droits au chômage. J’ai acheté 6 mois plus tôt un lot de 4 garages qui tourne bien. Je n’avais pas fait de crédit pour ce premier investissement immobilier.
Faire cet investissement locatif dans 50 garages sans revenus fixes a été une belle galère. Pour analyser ta situation, les banques regardent plus tes revenus personnels que les futurs revenus locatifs.

Pour bien faire, il faudrait presque que les revenus de ton travail couvrent le prêt à eux seuls. Les revenus prévisionnels quand tu achètes pour louer ne sont pas toujours pris en compte.
Par chance, et aussi par obstination, j’ai trouvé un jeune directeur d’agence qui m’a prêté 50 % de l’argent dont j’avais besoin. Trouer un crédit immobilier sans CDI a été possible uniquement parce que j’avais beaucoup d’argent de côté : 45000 €.
N’ayant pas de revenus fixes à long terme, il a fallu réduire le risque de la banque. Si elle ne finance que 50 % de la valeur du bien, elle est quasiment certaine de ne pas perdre d’argent. Si je ne rembourse pas les mensualités, la banque saisira le bien et le vendra aux enchères. Il est certain qu’elle vendra l’investissement locatif pour au moins 50 % du prix que je l’ai acheté.
Les banques ont peur de prêter pour des investissements locatifs aux personnes sans argent et sans revenu. En cas de pépin sur l’investissement locatif, elles craignent que l’emprunteur soit démuni financièrement et ne puisse pas régler le problème.
Pour trouver un prêt immobilier sans apport, il faudra souvent avoir un CDI ou du moins des revenus stables. En prime, la banque étudiera l’argent sur tes comptes. Investir en immobilier sans argent de côté sera extrêmement difficile.
Il te faut soit des revenus stables, de type CDI ou de l’argent de côté pour trouver un emprunt pour investir dans le locatif. Le moyen le plus simple d’investissement dans du locatif sans apport est d’avoir de l’argent de côté ET un CDI.
Investir dans le locatif sans CDI n’est pas facile. J’ai perdu beaucoup de temps à rencontrer les banquiers pour essuyer des refus. Ce n’est pas agréable, mais je croyais en mon projet. Être sans revenu, ni CDI ne m’a pas empêché d’obtenir un crédit immobilier pour investir. Ceci dit, je dois faire partie des exceptions.
J’aime autant être franc avec toi sur ce point. Il est beaucoup plus simple d’investir dans l’immobilier locatif sans apport que sans CDI.
Peux-tu acheter un appartement sans CDI ?
J’ai acheté un lot de 50 garages à 90000 € sans CDI puisque j’étais au chômage. Si tu veux acheter un appartement pour le louer, la logique sera la même que pour mon investissement.
Tu peux tout à fait acheter un appartement sans CDI. Je connais beaucoup de personnes qui ont investi sans CDI. La recette est souvent la même : une stabilité de revenu et/ou de l’argent de côté.
Tu peux être intérimaire depuis 5 ans et trouver un prêt immobilier pour investir sans CDI. La banque regardera la stabilité de tes revenus et l’absence de découvert. Si c’est le cas, alors tu pourras investir sans CDI.
Mettre de l’argent de côté alors que tu n’es pas en CDI est aussi un bon indice pour la banque de ta capacité à gérer tes comptes. Plus tu épargnes et plus la banque te fera confiance malgré l’absence d’un contrat à durée indéterminé.
Le CDI n’est pas le passeport magique indispensable à tout investissement locatif. Tu peux acheter un appartement, une maison voir même un immeuble sans CDI si tous les autres voyants sont au vert.
La méthode pour trouver un prêt immobilier locatif sans apport
Acheter pour louer avec ou sans apport ?
Si tu n’as pas d’argent de côté, alors la question ne se pose pas. Tu vas emprunter pour louer sans apport. Investir sans argent est impossible. Si tu n’as pas d’argent sur tes comptes en banque, alors tu as besoin d’argent pour investir.
Investir dans l’immobilier sans argent est possible grâce au crédit bancaire. Les crédits immobiliers permettent aux investisseurs sans argent d’acheter des biens immobiliers pour les louer.
Comment investir en immobilier sans argent ?
Investir dans l’immobilier sans argent est possible. Je pense à tous les jeunes couples qui achètent leur premier appartement ou leur première maison à crédit. Jamais ils n’ont l’argent sur leur compte pour payer l’appartement cash. Ils « investissent » dans leur résidence principale sans argent et à crédit.

La banque peut te permettre d’investir dans l’immobilier sans argent. Comment investir sans argent ? Le risque n’est-il pas trop grand pour la banque ?
En fait, la banque va se contenter de deux promesses. La première est ta capacité à la rembourser petit à petit pendant deux dizaines d’années environ. La seconde promesse est de saisir le bien pour le revendre si tu n’honores pas la première promesse.
On comprend vite qu’investir dans l’immobilier sans argent est possible à condition que la banque croit en tes capacités à rembourser tes dettes. Tu n’as pas besoin d’avoir d’argent maintenant pour peu que tu puisses générer des revenus réguliers pour rembourser les mensualités.
Le financement des investissements locatifs sans apport
Tu as vu qu’il est tout à fait possible de financer un investissement locatif sans apport. Ta capacité d’apport est l’argent dont tu disposes pour investir. Tu peux avoir 5 ou 10000 € épargnés sur un compte en banque. La première étape pour investir sans apport consiste à faire le tour de tes apports potentiels.
Il arrive souvent que cet apport soit très faible. Tu es étudiant et tu n’as pas encore de revenus. Tu es jeune actif et tu encaisses tes premiers salaires. Tout content de ce nouvel argent, tu décides de te faire plaisir et n’épargnes pas pendant quelques mois.
Mais il n’y a pas que les jeunes qui veulent investir sans apport. Tu peux aussi être plus âgé et prendre conscience que ta retraite sera en péril. L’investissement dans l’immobilier semble intéressant mais tu n’as pas mis d’argent de côté pour l’instant. Tu peux sortir d’un divorce avec beaucoup moins d’épargne que tu n’en avais.
Les raisons pour lesquelles tu n’as pas ou peu d’apport avant d’acheter un investissement locatif sont nombreuses. Malgré cela, les banques ont besoin de te prêter de l’argent pour en gagner. Il va donc falloir les rassurer.
Lorsque tu souhaites développer ton patrimoine, l’apport est le bienvenue. Investir avec un apport permet de rassurer les banques. D’une part, c’est une preuve que tu gères bien ton argent. D’autre part, cela réduit le risque de la banque.
Investir avec un apport permet souvent d’obtenir un crédit moins cher car le risque de la banque est moindre. Sa rémunération diminue en fonction de son risque. Plus tu apportes et plus ton dossier est solide, plus le taux du crédit et le coût du crédit seront faibles.
Pourquoi faire un apport lors d’un prêt immobilier locatif ?
Selon la période économique, les banques prêtent de l’argent plus ou moins facilement. Plus la période est tendue et plus elles ont peur d’accorder des crédits. L’apport devient un sésame pour ouvrir les vannes du crédit immobilier.
J’utilise parfois mon épargne pour investir dans les projets locatifs. Mon épargne est souvent mal rémunérée car je la veux disponible. C’est sans doute un tort de ma part. Pour combler cette (presque) absence de rendement sur mon épargne, je finance souvent la partie travaux de mes investissements dans les garages.
Je vais financer entre 10 % à 20 % de l’investissement locatif total. Sauf lors de mon achat de 50 garages, c’est toujours moi qui choisit si je fais un apport pour le crédit investissement locatif. Depuis quelques années, les banques m’aiment beaucoup et je suis en mesure de négocier avec elles.
Il y a un achat immobilier pour lequel je ferai un apport conséquent sans hésiter. C’est pour acheter ma résidence principale. Je n’ai pas envie de m’endetter sur 20 ans pour notre maison. Si je peux payer cash ma résidence principale, alors je ferai ce choix.

Pourquoi faire un apport important et pas un crédit immobilier pour acheter sa résidence principale ?
Imagine que tu trouves la maison ou l’appartement de tes rêves. Le prix négocié est dans ton budget : 200000 €. Tu vas voir ta banque et elle te prête sur 20 ans contre une mensualité de 1000 €. C’est conforme à ton budget et tu achètes la maison.
En passant, la banque n’a pas vraiment insisté sur le coût du crédit. Il est possible selon les taux et la durée que tu paies 50000 à 70000 € d’intérêts et frais divers. Au final, la maison ou l’appartement te revient à 250000 €, soit 25 % plus cher à cause de l’emprunt.
Si tu achètes le même appartement pour le louer, le coût du crédit est beaucoup plus faible même si la banque te prête au même taux et dans les mêmes conditions.
La déduction des intérêts d’emprunt dans un investissement locatif
Eh oui, quand tu déclares tes revenus immobiliers aux impôts, tu peux déduire les intérêts facturés par la banque pour ton emprunt dans le cadre d’un investissement locatif. Cette déduction est très intéressante et j’en profite au maximum.
Reprenons notre exemple. Tu loues l’appartement en location nue et déclares tes revenus dans la catégorie des revenus fonciers. Ta tranche marginale d’imposition est de 30 % et la CSG CRDS est de 17,2 % fin 2018.
Le loyer annuel de l’appartement est de 10000 €. Tu vas donc payer 10000 € x (30 % + 17.2 %) = 4720 € d’impôt.
Le coût du crédit immobilier est de 50000 € sur 20 ans, soit 2500 € par an (50000 / 20 ans).
Les intérêts d’emprunt pour un investissement locatif sont déductibles des revenus. Au lieu de déclarer 10000 € de loyers, tu déclares 10000 – 2500 € d’intérêts, soit seulement 7500 €. Tu vas payer 7500 € x (30 % + 17.2 %) = 3540 € d’impôts.
Au final, grâce à cette défiscalisation des intérêts d’emprunt dans l’immobilier locatif, tu économises les impôts sur les intérêts du crédit. Dans notre exemple, tu économises 50000 € x (30 % + 17.2 %) = 23600 € d’impôts.
A choisir, tu comprends que je souhaite défiscaliser les intérêts de mes crédits immobiliers dans l’investissement locatif. C’est pour cette raison que j’emprunte sans apport ou avec peu d’apport pour investissement dans le locatif.
Je préfère mettre de côté mon épargne et réaliser un gros apport dans l’achat de ma résidence principale où je ne pourrais pas déduire les intérêts de l’emprunt de mon imposition.
Comment financer un investissement locatif sans apport ?
Financer un investissement locatif sans apport sera plus compliqué. Il faudra montrer patte blanche avec un dossier impeccable. Un beau et bon dossier de présentation fait souvent bonne impression. Cela prouve que tu as pensé ton investissement immobilier sous tous les angles.

La banque aime que l’investisseur prenne en compte les risques de son projet et les scenario qui peuvent se produire. La connaissance des frais, de la fiscalité, des assurances, taux d’endettement, taux de rendement, etc, etc, te feront paraître professionnel aux yeux du banquier. Je te conseille de lire cet article sur le calcul du taux d’endettement pour les investisseurs immobiliers. C’est sans doute l’une des clés pour investir dans l’immobilier avec un crédit sans apport.
La patience et la persévérance sont de mise car certaines banques seront sourdes à tes demandes si tu n’apportes pas d’argent dans le projet locatif. Le jeu en vaut souvent la chandelle.
Quels investissements locatifs se financent sans apport ?
Si tu trouves des investissements immobiliers en autofinancement, alors investir sans apport sera plus facile. Pour rappel, un investissement locatif autofinancé est le graal.
Les loyers (1000 €) couvrent la mensualité de crédit (500 €), les charges et taxe foncière (200 €) et les impôts (200 €). Il reste donc 100 € chaque mois à l’investisseur. On appelle cela un cash-flow positif.
Avec un investissement autofinancé par le locataire, le prêt ou le crédit sera obtenu plus facilement car le risque pour la banque et l’investisseur est minime.
Les parkings et les garages sont souvent en autofinancement car ils affichent des très beaux rendements. Acheter une place de parking à l’unité ne permet que rarement d’atteindre l’autofinancement. Investir dans des lots de garages est plus simple de ce point de vue.
Par contre, financer un parking à crédit sans apport est plus simple car les montants à investir sont souvent inférieurs à 20000 €. Le risque pour la banque est faible et elle tend à financer toute l’opération sans demander d’apport à l’investisseur immobilier.
Les appartements loués en meublé courte durée ou en colocation affichent eux aussi des rendements élevés. L’autofinancement sera plus facile à atteindre et le crédit locatif sans apport te tend les bras. Attention, l’investissement en meublé est souvent chronophage. Cela peut devenir un second métier.
Les immeubles de rapport en campagne offrent aussi des rendements et des montants d’investissement qui permettent parfois d’emprunter sans apport. Acheter un immeuble locatif sans apport demande un dossier impeccable et surtout une expérience de la part de l’investisseur immobilier. Le risque d’acheter un immeuble de apport est important, alors la banque aura plutôt tendance à demander un apport avant de prêter.
Peut-on acheter de l’immobilier locatif sans CDI et sans apport ?
Peut-on acheter des investissements locatifs parking sans apport ?
Investir dans un parking demande moins d’argent que pour investir dans un appartement. Cependant, tu as souvent besoin d’utiliser un crédit pour acheter un parking ou plusieurs garages. Il y a des questions que les lecteurs me posent souvent au sujet des crédits.
Faut-il mieux acheter à crédit avec ou sans apport ? Qu’est-ce que le TEG ? Sur combien de temps emprunter ? Qu’est-ce que le cashback ? J’écris cet article pour répondre à ces questions.
Pourquoi investir dans un parking à crédit et sans apport ?
La raison principale pour laquelle tu dois utiliser le crédit et investir dans le locatif sans apport est avant tout financière. Si tu veux t’enrichir, tu es obligé de faire appel au crédit. Je m’explique. Pour acheter un lot de garages vendu 300 000 €, il est peu probable que tu aies l’argent disponible sur ton compte en banque.
Tu fais donc appel au crédit pour acheter le bien, ta résidence principale, un appartement ou un parking. Tu deviens alors propriétaire beaucoup plus tôt que si tu devais attendre d’avoir la somme en entier sur ton compte en banque. La plupart des investisseurs font donc appel au crédit pour s’enrichir plus rapidement.
Investir sans apport permet d’acheter du locatif beaucoup plus tôt. Si tu dois attendre d’avoir 20 % du montant à emprunter, il te faut patienter deux ou trois ans ou plus entre chaque investissement locatif. Acheter de l’investissement immobilier sans apport permet d’augmenter le rythme de tes investissements locatifs.
Acheter plus tôt permet de bénéficier de l’augmentation des prix de l’immobilier. Le marché connaît bien sûr des hauts et des bas. Les prix varient beaucoup d’une région à une autre. Nous ne savons jamais si les prix de Paris par exemple, vont rester à ce niveau, ou si nous sommes dans une bulle spéculative.
Je crois profondément à une tendance haussière des prix avec des variations sur des périodes décennales. Si tu connais des personnes qui ont acheté leur maison avant les années 90, ils t’ont surement raconté l’excellente plus-value qu’ils ont réalisé en revendant 10 ans plus tard.
Crois-moi, s’ils avaient dû attendre d’avoir 100 % ou 50 % d’apport sur leur compte pour acheter en l’an 2000, ils ne seraient toujours pas propriétaire. La faute à qui ? A l’inflation pardi ! Les actifs immobiliers protègent les investisseurs contre l’inflation.
Dernier argument en faveur du crédit, c’est son coût souvent minime. Pour un emprunt de 100 000 € sur 15 ans à 3.65 % TEG, le coût est de seulement 30 000 €. Cela revient à 2000 € par an en moyenne. Si les prix de l’immobilier augmentent de 2 % en moyenne par an (j’enlève l’effet des intérêts cumulés), ton bien gagne lui aussi 2000 € par an. Au final, le crédit ne te coûte rien !
Tu peux faire appel à une banque pour financer ton investissement dans les parkings. Il existe aussi des organismes de crédit en ligne et des courtiers en crédit. Les courtiers peuvent être tout à fait avantageux pour toi. Pour des investissements en dessous de 70 000 €, leurs frais seront trop élevés.
Comment choisir le montant de l’apport dans ton crédit locatif ?
Choisir son crédit locatif avec ou sans apport est avant tout une question d’objectif personnel. Je ne ferai pas le même choix que toi, car mes objectifs de vie, de projet, sont tout simplement différents. Mon second investissement s’autofinancait totalement à crédit. J’ai toutefois réalisé un apport de 45000 € en complément du prêt locatif.
Ainsi, j’ai un revenu de 4000 € net d’impôt disponible tous les ans. Les revenus du blog sont variables et je ne sais pas quand je pourrai réinvestir dans les parkings. Pour me sentir plus libre et moins contraint, j’ai donc choisi un financement locatif plus faible et un montant d’apport plus important. Note aussi que je n’ai pas eu beaucoup de choix non plus comme expliqué plus haut.
La durée du financement varie aussi selon tes objectifs. Si tes enfants font des études coûteuses dans 15 ans, tu seras content si ton crédit se finit un an avant le début de leurs études. Tu pourras ainsi profiter de l’intégralité des loyers pour payer leurs logements et leurs frais divers. Réaliser un apport au moment de signer ton crédit immobilier permet de raccourcir la durée du prêt.

Plus la durée d’un emprunt est courte, moins le risque est grand pour la banque. En conséquence, son coût diminue aussi. Prendre un crédit sur des durées supérieures à 20 ans augmente beaucoup le coût du crédit en comparaison avec la diminution relative des mensualités. Il faut parfois faire un apport supplémentaire pour réduire le coût final du crédit locatif.
Quoiqu’il en soit, toutes ces considérations sont complexes, et je te conseille de bien prendre en compte tes objectifs dans tes calculs de rendement.
Choisir ton prêt pour un investissement locatif
Pour choisir ton crédit immobilier locatif, je te conseille de comparer le Taux Effectif Global. Je ne te détaille pas la formule exacte, car elle est extrêmement complexe. Pour la résumer, c’est le coût total de ton crédit pour ton investissement locatif. Il prend en compte les frais de dossier, le coût de la garantie, les assurances, le taux nominal, bref, tout ce que va te coûter ton crédit. C’est ce taux avec lequel tu vas comparer les offres de prêt entre elles. Plus le TEG est bas, meilleures sont les conditions de ton crédit.
Je nuance toutefois ce propos, car il faut tenir compte du type de garantie et du contrat d’assurance. Il vaut mieux payer un peu plus cher ton crédit, avec une garantie plus souple, des conditions de modulation des mensualités et une assurance qui couvre bien les aléas de la vie.
Pour répondre aussi à la question d’un lecteur, voici ce que veux dire le cashback. En français, cela se traduit par retour de l’argent. Prenons un exemple : tu achètes un lot de parking 100 000 €. Son rendement net de charges et d’impôts est de 5 %. Ce taux signifie que chaque année, une fois les charges et les impôts payés, tu vas encaisser 5 % de 100 000 €, soit 5000 €. Le cashback répond à la question suivante : combien d’années te faut-il pour récupérer la somme que tu as investi dans ce parking ?
Bref, combien d’années de bénéfices à 5000 € te faut-il attendre pour récupérer tes 100 000 € ? Réponse : 100 000 € / 5 000 € = 20 ans. Il te faut donc attendre 20 ans. C’est la durée de ton cashback. C’est aussi un élément à prendre en compte lorsque tu souscris un crédit. Plus ton cashback est long, moins bon sera ton investissement.
4 raisons de réaliser des investissements locatifs à crédit
Avant de te donner des clés pour comprendre le fonctionnement des crédits immobiliers dans le cadre des investissements locatifs, je veux revenir sur les avantages des investissements locatifs.
Je suis fan de l’investissement locatif sans apport et des avantages qu’il procure. Avant de se lancer dans des investissements locatifs, il faut y penser à deux fois. En effet, les sommes en jeu sont importantes et un investissement locatif dure plusieurs années. Tu vas maintenant apprendre les trois principales raisons qui me motivent (et toi aussi sans doute) à continuer dans l’investissement locatif.
L’investissement locatif est simple
Un investissement locatif, c’est très simple. Tu achètes un bien immobilier. Tu le loues à un locataire en échange de loyers. Ces loyers sont tes revenus locatifs. Même un enfant de 10 ans est capable de le comprendre. Et il est facile de faire, ou de refaire quelque chose que tu as bien compris.
Avec la bourse, j’ai toujours eu plus de mal. Au delà de mon premier investissement boursier dans Eurotunnel qui m’a fait perdre une bonne moitié de mon investissement, j’ai du mal à concevoir le fonctionnement des dividendes, des cours de l’action etc etc… Alors qu’avec l’immobilier, c’est beaucoup plus simple.
Investir dans l’immobilier locatif avec ou sans apport est terre à terre : tu achètes quelque chose de physique pour le louer. Acheter une maison, un appartement, un garage, un local commercial pour les louer est relativement simple. Ce sont des surfaces destinées à être louées, mais tu peux t’en servir pour ton usage personnel. En cas de malheur (crise économique, guerre…), ce que tu possèdes aura souvent une valeur physique.

Est-ce qu’un billet de banque aura toujours une valeur ? Ce n’est pas si sûr ! La valeur d’un billet n’est pas dans le coût du papier et l’encre qui le compose mais dans la croyance que l’Etat garantit sa valeur. L’avantage des investissements locatifs immobiliers : ce sont des actifs tangibles, physiques, réels, avec une valeur intrinsèque (comme l’or, l’argent qui auront toujours une valeur).
Le crédit finance les investissements locatifs avec ou sans apport
« Les investisseurs boursiers peuvent et doivent apporter leur contribution à cet article dans les commentaires, merci d’avance ! »
La plupart des achats locatifs se font à crédit. Tu pousses la porte d’une banque. Tu rencontres le conseiller pour lui parler de ton projet et de tes besoins financiers. La banque t’accorde un crédit et tu deviens propriétaire. Enfin, non, la banque devient propriétaire de ton logement jusqu’à la fin de ton prêt. N’empêche que tu jouis de ce bien immobilier alors que tu n’as pas déboursé un centime (ou presque) !
Dans les faits, le financement immobilier sans apport et total, c’est à dire le bien immobilier plus les frais de notaire existe, mais ce n’est pas systématique. Quand je suis allé voir mon banquier pour acheter mon lot de 50 garages à crédit, il m’a dit qu’il demandait 25 % d’apport en moyenne pour des investissements locatifs.
Imagine que tu n’aies pas accès au crédit, ou qu’il n’existe pas. Comment de temps faudrait-il que tu économises pour acheter ta résidence principale ? Dans la plupart des cas, je pense que nous deviendrions propriétaires autour de 50 ou 60 ans, voir jamais.
Attendre d’avoir la somme dans son entier pour acheter un bien immobilier est long, trop long. L’investissement locatif a pour avantage de se faire à crédit, voire sans apport. Bien souvent, tu ne paies que les frais de notaire et le reste est financé par la banque. Avec la bonne méthode et un bon dossier, tu peux trouver un prêt immobilier sans apport. Ton locataire te paie les loyers et ceux-ci remboursent le prêt.
Trouver un prêt immobilier locatif sans apport
As-tu déjà demandé à ton banquier un prêt pour investir en Bourse ? Je ne l’ai pas testé, mais voici le problème qui se pose au banquier. Un prêt est garanti par une contrepartie. La banque doit pouvoir se rembourser de l’argent qu’elle a prêté si l’emprunteur fait défaut. La contrepartie d’un investissement locatif est donc le bien immobilier. C’est quelque chose qui est tangible, physique dont le prix varie, mais sur des périodes longues. La banque pourra revendre le bien.
Avec une action, c’est très difficile de prévoir le cours de l’action à coup sûr pendant 10 ans. De plus, cela ne constitue pas une garantie valable aux yeux de la banque. Donc pour investir en Bourse, il faut avoir du cash, de l’argent sur son compte en banque. Cela limite forcément le montant que tu vas investir.
Dans l’immobilier locatif, tu peux investir beaucoup plus que l’argent dont tu disposes et même parfois sans apport. Lors de mon investissement locatif dans 50 garages en Normandie, je n’ai apporté en cash « que » la moitié des 90000 €. J’ai pu investir 90000 € et je reçois les loyers en conséquence alors que je n’ai payé « que » la moitié des garages. Cela s’appelle l’effet de levier.
Pour conclure, l’avantage de l’investissement locatif est qu’il peut se faire à crédit. Tu peux investir plus tôt et avec des sommes plus importantes que si tu devais économiser avant d’investir.
L’investissement locatif permet de vaincre le marché
Je vais encore reprendre l’exemple de la Bourse. Quand tu achètes une action, tu l’achètes au même prix que tous les acheteurs (qui investissent à la même heure que toi). Idem, quand tu revends la même action, le prix est fixé par le marché. Bien entendu, il existe de nombreuses personnes qui s’enrichissent avec ce levier. Ces investisseurs savent quand acheter des actions en bourse au plus bas et revendre au bon moment, en réalisent une plus-value au passage. Bravo à eux !
Dans l’investissement locatif immobilier, tu as un avantage supplémentaire par rapport à la Bourse. Le prix d’achat et le prix de vente d’un bien immobilier n’est pas fixé par un cours, mais il est fixé d’un commun accord entre l’acheteur et le vendeur.
Dans un achat ou dans une vente, il y a souvent une marge de négociation. Il est possible d’acheter un bien immobilier en décalage avec son prix de marché. Cela est impossible en Bourse ! Voici un exemple : Deux acheteurs peuvent investir dans deux appartements situés dans le même quartier, avec les mêmes caractéristiques pour un prix totalement différent.
Un avantage de l’investissement locatif immobilier est de profiter de ces écarts de prix. Tu peux tout à fait acheter à un prix plus bas que la valeur réelle. De la même façon, tu peux revendre à un prix plus élevé que la valeur du marché.
La rentabilité moyenne dans l’immobilier classique est d’environ 4 %. Là encore, c’est une moyenne. L’investissement dans les parkings lui tourne autour de 7%-8% brut. Tu obtiendras davantage des rendements supérieurs à l’investissement locatif classique.
Pour résumer, les avantages de l’investissement locatif immobilier sont les suivants :
- un concept simple basé sur un actif tangible
- la possibilité d’investir plus d’argent et plus tôt grâce au crédit
- l’achat et la vente ne se font pas toujours au prix du marché
- obtenir des performances plus fortes que la moyenne
Après ce point sur les quatre motivations qui me forcent à investir à crédit, voici comment les prêts pour l’immobilier locatif fonctionnent.
Comprendre le calcul des intérêts d’emprunt pour un achat immobilier locatif
Si tu lis ces lignes, alors il est probable que tu t’intéresses à l’argent et par la même occasion aux mensualités de crédit. Nous sommes une minorité à nous intéresser à ce sujet. La majorité des personnes ne se forme pas sur ce domaine. Seulement deux millions de ménages français possèdent un ou plusieurs logements locatifs. Un très petit nombre d’entre eux achète uniquement des parkings ou des boxes.
J’ai commencé à m’intéresser à l’argent par hasard. Lors de mes études, j’ai dû passer un semestre à l’étranger. C’est alors que j’ai choisi d’étudier à Montréal. Dans les universités du système anglo-saxon, je pouvais choisir quatre cours à étudier pendant ce semestre.
Un cours a particulièrement retenu mon attention. C’était un cours de finance personnelle. Mais qu’est ce que c’est ? Les finances personnelles sont une manière de désigner la gestion de l’argent à titre privé.
J’ai donc eu le plaisir de suivre quatre mois de cours intensif sur la gestion de l’argent. Mais pas l’argent au sein d’une entreprise… juste comment gérer mon argent à titre personnel.
Les mathématiques financières à la rescousse
Il y a des notions tout à fait basiques que Monsieur et Madame Tout le monde connaissent. Si tu dépenses plus d’argent que tu n’en gagnes, alors tu perds de l’argent chaque mois. A l’inverse, si tu as des revenus supérieurs à tes dépenses, tu gagnes de l’argent.
Ainsi l’argent supplémentaire qui te reste à la fin de chaque mois peut être utilisé de beaucoup de manières. Tu peux par exemple l’épargner. Épargner veut dire mettre de l’argent de côté. Cet argent est mis sur un ou plusieurs comptes bancaires pour servir à réaliser des projets, préparer un investissement, préparer sa retraite etc etc… Quand ton argent est épargné, la banque ou l’organisme financier te verse des intérêts.
Si tu épargnes 1000 € sur un livret A, la banque te reverse 1.25 % par an en guise de rémunération de ton épargne. On appelle taux d’intérêt le pourcentage que la banque te donne pour ton épargne. La banque te paie pour avoir le droit d’utiliser ton épargne.
Si tu places 1000 € pendant un an à 2 % d’intérêt, tu gagnes donc 2 % x 1000 € = 20 €. Le calcul est assez simple. Voyons maintenant ce qui se passe si tu laisses ces 1000 € pendant 5 ans dans la même banque.
| Capital | Intérêts | |
| Début d’année 1 | 1000 € | 20 € |
| Fin d’année 1 | 1020 € | 20,4 € |
| Fin d’année 2 | 1040,4 € | 20,8 € |
| Fin d’année 3 | 1061,2 € | 21,2 € |
| Fin d’année 4 | 1082,4 € | 21,6 € |
| Fin d’année 5 | 1104 € |
Tu vois bien que les intérêts ne sont pas restés les mêmes d’une année sur l’autre. Ils augmentent un petit peu chaque année. C’est la magie des intérêts composés. Si tu laisses tes intérêts sur ton compte épargne, les intérêts sont pris en compte dans le calcul de la rémunération que la banque va te verser.
Le formule mathématique pour trouver le montant du capital en année X, sans passer par mon tableau est la suivante :
Capital année X = capital année Y x (1 + taux d’intérêt) ^(année X – année Y)
Dans mon exemple : capital année 5 = 1000 € x (1+2 %) ^ 5 = 1104 €. Les amateurs de produits boursiers sont familiers de cette formule. Quand tu réinvestis tes dividendes pour acheter une action, tu utilises la rémunération (le dividende remplace le taux d’intérêt bancaire) de ton portefeuille boursier pour créer des intérêts composés. C’est la première notion que j’ai appris dans le cours de finance personnelle.
Les mensualités dans un crédit immobilier
J’ai aussi beaucoup appris sur les fonctionnements des crédits. A l’époque, je pensais que si j’empruntais 100000 € sur 20 ans, j’allais rembourser 5000 € par an. Cependant, mon raisonnement était faux car j’avais oublié le coût du crédit.
Quand tu achètes un parking à crédit, la banque te facture des frais de dossier. C’est une somme fixe que tu paies au début de ton crédit. Puis tu vas payer des intérêts sur la somme que tu empruntes.
Imagine que tu empruntes 10000 € à 4 % sur 5 ans. Vas-tu payer
- 10000 € x 4 % = 400 € d’intérêts ou
- 10000 € x 4 % x 5 ans = 2000 € ?
Les deux raisonnements sont faux ! Tu vas payer 1050 € d’intérêts.
La formule pour le calcul des intérêts d’un emprunt immobilier
La formule n’est pas aussi simple que je ne le pensais. Les 4 % d’intérêts sont appliqués sur le montant du capital restant dû. Le calcul se fait en deux temps :
- on calcule le taux d’intérêt mensuel 4 % / 12 = 0.33 %
- on calcule les intérêts à payer le premier mois : 10000 € x 0.33 % = 33,33 €.
La mensualité pour un crédit de 10000 € à 4 % TEG sur 5 ans est de 184 €. Tu rembourses 184 € à ta banque tous les mois pendant la durée du crédit. Dans ces 184 € versés le premier mois, tu paies 33.33 € au titre des intérêts (la rémunération du prêteur) et 184 € – 33,33 € = 151 € de capital. Tu as remboursé 151 € sur les 10000 € que la banque t’a prêté.
On calcule ensuite les montants des intérêts du deuxième mois :
Intérêts à verser = Capital restant dû x taux d’intérêt mensuel
soit (10000 € – 151 €) x 0.33 % = 32.83 €. Et ainsi de suite… Le montant des intérêts dans la mensualité (toujours fixe d’un mois à l’autre) diminue. C’est pour cette raison que tu pourras déduire beaucoup d’intérêts lors des premières années de ton prêt immobilier. Les intérêts sont toujours forts au début et vont en diminuant, car tu rembourses toujours plus de capital à mesure que tu avances dans le temps.
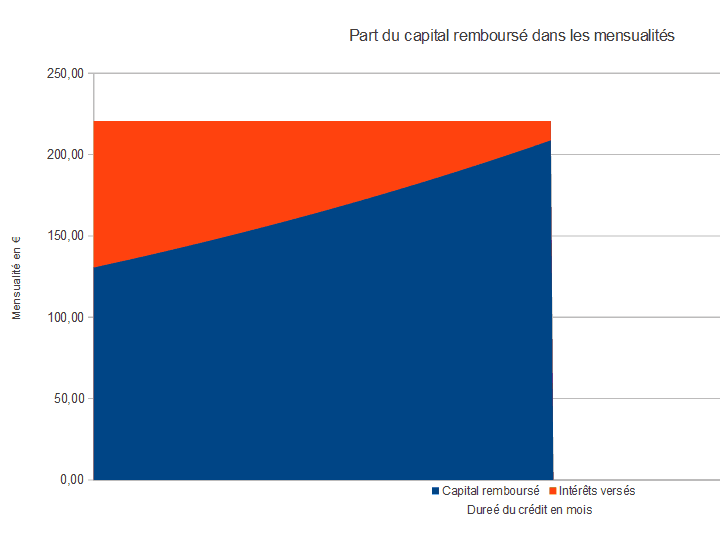
Le calcul du montant d’intérêt est relativement simple. La somme empruntée est toujours la même. D’ailleurs, la banque te fournit le détail des mensualités avec la part d’intérêt et la part de capital que tu vas rembourser pour chaque mensualité pendant la durée de ton crédit.
Le calcul devient plus complexe quand la somme empruntée n’est pas fixe. C’est souvent le cas avec les cartes de crédit que tu peux acheter en grande distribution. Ces cartes te permettent d’avoir un capital immédiatement disponible. Imaginons que tu souscrives à une offre de crédit renouvelable. C’est à ce moment là que la banque évalue ton dossier et décide de mettre 5000 € à ta disposition.
Tu peux faire un premier achat de 1000 €. La banque calcule alors une mensualité sur les 1000 € de capital que tu as emprunté. Tu commences à rembourser une part d’intérêt et une part de capital chaque mois. La formule reste la même :
Intérêts à verser = Capital restant dû x taux d’intérêt mensuel
Si tu fais un second achat de 3000 € 6 mois plus tard, le calcul est mis à jour car le montant emprunté n’est plus le même. Le capital restant dû est égal à : 1000 € – la part de capital déjà remboursé + 3000 €. Le calcul se complexifie car le capital emprunté peut varier. Finalement, c’est pour cette raison que les organismes de crédit renouvelable sont obligés d’informer leurs clients chaque mois du calcul de leur crédit.
Petit clin d’œil
Tu sais maintenant comment sont calculés les mensualités d’un emprunt bancaire. Une mensualité est un montant fixe à l’intérieur duquel le pourcentage de capital remboursé et d’intérêts payés varie chaque mois.
Les intérêts sont forts en début de crédit, quand le capital restant dû est important. En revanche, les intérêts sont faibles en fin de crédit, quand le capital restant dû a bien diminué.

Pour finir, voici une photo souvenir de mon week end parisien. Regarde qui j’ai croisé dans les allées de Roland Garros ce dimanche 😉
Je te laisse deviner qui a reconnu l’autre 😉








Bonjour,
Merci pour ce site tres interessant.
Petite question qui a deja été posée mais non répondue : Si l’on possède la somme pour acheter un garage (ex : 15K€) est-il necessaire de faire un crédit malgré tout ?
Merci bien et bravo à vous
Bonjour,
non, le crédit n’est pas obligatoire. Il peut être un avantage ou un inconvénient selon les situations.
Bonjour
oui je vois des avantages à l’investissement locatif. Moi j’investis plutôt dans le saisonnier mais il y a beaucoup de similitudes. La rentabilité est bonne et plus rapide que pour d’autres investissements. Il faut avoir un esprit positif!
Yanoudomino
Bonjour,
oui, je suis d’accord avec toi, les rendements sont aussi corrects dans la location saisonnière. Mais attention car c’est très chronophage et la loi ALUR a changé les règles du jeu !
Bonjour Julien,
Dans ma situation j’ai la possibilité d’obtenir un crédit sans intérêts en empruntant à une personne de ma famille qui est prête à m’aider à faire mes premiers investissements locatifs.
Sais tu si je pourrais déduire de mes futurs revenus fonciers les mensualités que je vais devoir lui rembourser sachant que le prêt viendrait donc d’un particulier et non pas d’une banque ?
Merci d’avance pour ta réponse et surtout pour la mine d’informations qu’est ton site.
Bien cordialement
Bonjour Pierre,
non, tu ne pourras pas déduire tes mensualités de tes revenus locatifs dans ton cas…
Bonjour,
Excellente démonstration. Il est clair que plus le capital mis en épargne est élevé, plus élevé sera la somme que tu percevras rajouté aux intérêts. Le mieux est de pouvoir augmenter ce capital en injectant autant que l’on peut dès que l’occasion se présente.
Salut Julien,
Une article vraiment très pédagogue.
Même si je maitrise les concepts dont tu parles j’ai parcouru l’article en entier tant il se lit facilement.
Il est très important de savoir comment fonctionnent les taux d’intérêts aussi bien pour l’épargne que pour les dettes.
On peut ainsi voir qu’il vaut mieux rembourser rapidement les dettes avec un fort taux d’intérêt. Et qu’il est préférable de réinvestir ses gains pour profiter d’un bel effet boule de neige.
P.S.: Sympa ta photo 😉
Marc.
Bonjour,
Visiblement tu n’as pas été super assidu lors de ta formation.
Déjà tu oublies de préciser que tu parles d’un crédit amortissable. Pour un crédit in fine c’est différent.
Mais plus grave pour calculer les intérêts tu parles du TEG mais c’est le taux nominal qu’il faut prendre pas le taux effectif global !
Bonjour Didier,
re voilà le spécialiste du crédit et de l’immobilier.
Merci pour tes précisions inutiles.
Tu as (encore) raté l’essentiel qui était d’expliquer pédagogiquement le fonctionnement d’un crédit.
Je n’ai pas validé tes liens…
Vu que tu poses la question, Stéphane Plaza aurait bien pu te reconnaître avant que toi tu le reconnaisse 🙂
Oui, cela aurait pu se passer comme cela, mais non 😉
bonjour, Julien,
ton raisonnement était tres clair.
Cependant, je crois me souvenir que, dans mon cas personnel (emprunt immobilier sur 15 ans, terminé/remboursé il y a bien longtemps) le calcul des mensualités à rembourser est parfois différent de celui que tu indiques: durant les 4 ou 5 premières années, on ne rembourse que des intérets… qui se calculent, hélas, sur la totalité du capital emprunté!
Je ne sais pas si cela se pratique encore?
cordialement,
jeancl2.
Bonjour Jean Claude,
je ne connais pas ce type de crédit. A-t-il un nom ?
Je pense que c’est interdit maintenant pour les banques, il faut maxi 50% d’intérêts sur une mensualité.
SALUT JULIEN
A mon avis c’est lui qui t’as reconnus et peut être même que tu lui a signé un autographe.
C’est ça 🙂
Superbe article !
Et oui, l’intérêt de s’occuper au maximum de ses finances personnelles avant d’investir est primordial. Au début, cela peut carrément être « mal vu » par l’entourage qui n’a pas l’habitude de voir une personne s’intéresser de près à ce sujet.
Si jamais les remarques fusent un peu trop, on peut répondre de la manière suivante :
« -Tu trouves que je m’intéresse beaucoup à l’argent ?
-Ah oui, tu fais que ça avec tes bouquins et tes trucs sur internet, ça va te rendre dingue.
-D’accord, c’est une manière de voir les choses…J’ai une question : Pourquoi te lèves-tu très tôt le matin tous les jours de l’année ? Tu passes plus de temps au boulot qu’avec ta propre famille, pourquoi ? Ne me répond pas, je sais que c’est pour gagner de l’argent et je ne te le reproche pas. Pour ma part je cherche simplement à trouver d’autres moyens que celui-ci pour gagner ma vie et essayer de me libérer plus de temps pour le passer avec ceux que j’aime. Au final, si j’arrive à mes fins, j’y penserai moins que toi 😉 »
C’est un exemple et pour l’avoir testé, c’est très efficace !
Merci pour le rappel sur le crédit bancaire. Hoooo le petit Stéphane était dans le coin !! Quel chance, il a l’air vraiment sympa ce gars.
Je pari que c’est lui qui t’a reconnu vu que tu deviens une petite célébrité !
Au plaisir,
Adam
Salut Julien,
Géniale cette photo ! Deux stars de l’immobilier 🙂
A bientôt,
Fabrice
superbe article
Hello, tes premières formules sont fausses, Capital n+1 = capital n * (1+tx)^durée
Ça se comprend mais bon…
Cordialement,
Julien
Salut Julien,
Merci beaucoup ! Il y a donc quelqu’un qui suit 😉
J’ai effectivement oublié le 1 dans (1+tx). Je l’ai pris en compte dans mes calculs, mais pas noté…
merci encore
salut julien ,
merci pour nous avoir expliquer comment sont calculés les mensualités d’un emprunt bancaire.qu’elle chance d’avoir rencontrer Stéphane plazza.
à bientôt
Jérôme
Salut Julien,
Un très bon article, comme d’hab 😉
Petites questions.
1) Dans l’article tu dis que pour des investissements inférieurs à 30 000€, il vaut mieux passer par des organismes de crédit en ligne.
Quelle durée de crédit préconises-tu ?
Car quand on regarde la TEG de ce genre d’opération elle s’envole 🙁 .
2) A partir de quel montant penses-tu qu’une banque peut suivre un investisseur de garages ?
Marc.
SAlut Marc,
1. ce n’est pas ce que j’ai écrit. Au dessous de 30/40 K€ un courtier n’est pas intéressant financièrement. Ses frais sont trop élevés.
2. Les banques financent des opérations tout simples, même à 5000 €.
quel type de crédit pour des petits montants?
Coucou Julien,
Avant toute chose, je tiens à te présenter mes félicitations concernant ton blog….merci de nous faire partager ton expérience et merci pour tes explications qui sont très claires et très précises.
Je fais suite à ton expo concernant l’achat à crédit.
Petite question sur le cashback : mieux vaut avoir une durée que cashback inférieur à la durée du crédit ou supérieur ?
Deuxième et dernière question (qui n’a d’ailleurs rien à voir avec le sujet) : par ton expérience, peux tu nous donner une mensualité moyenne d’une assurance d’un garage type box quand on est bailleur de garage ?
Dans l’attente d’une réponse de ta part,
Cordialement,
Steph.
Bonjour Steph,
merci pour ton retour.
Je ne compare jamais le cashback avec la durée du crédit… Ce n’est pas du tout la même chose. Avoir un cashback inférieur au crédit est d’ailleurs impossible il me semble.
Je n’ai pas de moyenne à te donner, si ce n’est que je paie 180 € par an pour mes 50 garages.
Bjr Julien,
Merci pour ta réponse.
Pour ce qui est de l’assurance, peux tu nous donner l’ensemble des garanties de ton contrat d’assurance et, si possible, le nom de l’assurance ? Pour etre clair, je suis en train de voir pour assurer une dizaine de garage type boxe que je veux louer : j’ai demandé à plusieurs assurances (locales et plateformes) et elles m’annoncent entre 2,5 euros et 4,5 euros par mois et par box !!!!! ce qui est très loin de tes 30 centimes par boxes !!!! Je sais bien que bcp de critères rentrent en ligne de compte pour ce qui est des tarifs d’assurance mais là, je suis assez étonné de tes tarifs !!!!
Dans l’attente d’une réponse de ta part.
Cordialement,
Steph.
Bonjour Steph,
je t’invite à m’envoyer un mail et je t’envoie cela en privé.
Bonjour Julien,
Article intéressant.
En effet, selon les situations le crédit va être plus ou moins avantageux. C’est donc du cas par cas.
Concernant un plus petit investissement (inférieur à 100 000 euros) et si l’on dispose de la somme nécessaire on peut se poser la question de payer cash afin de profiter des revenus mensuels directement.
La meilleure option reste pour moi celle-ci:
Achat à crédit d’un grand lot de garage aux alentours des 100K€ avec des revenus locatifs qui vont te permettre de régler tes mensualités et charges + un cashflow mensuel.
Là, on engage un crédit mais on gagne tout de suite de l’argent.
Adam
Merci Julien pour ton article 🙂
L’un des points majeurs retenu pour un investissement immobilier (parking, appartement, …) reste pour moi l’assurance des crédits immobiliers qui protège mes proches au cas où je disparaisse. En effet, mes proches récupèreraient mes investissements dont le reste à payer des crédits serait réduit à 0. Ceci n’existe pas dans les placements financiers qui nécessitent de mettre ses économies en bourse, assurance vie ou autres au fur et à mesure (à part récupérer la somme investie au jusqu’au du drame).
Le choix de l’assurance peut être important en fonction de l’activité professionnelle et loisirs à risques réalisés. Ne pas hésiter à choisir son assureur.
Autrement, vu le contexte économique de déroute des banques Grecques, nous ne sommes pas loin de rencontrer la même chose en France (ponctionnement d’un pourcentage sur les comptes des épargnants) ! Donc je privilégie ma faible exposition aux comptes garnis 😉
Salut Loïc,
oui, c’est un des points forts des investissements immobiliers. Le risque de décès est nul en cas de crédit assuré à 100 %, et les héritiers sont couverts.
Ne sois pas trop péssimiste, j’espère qu’il n’y aura pas de ponctionnement en France…
salut julien,
quand on utiliser l’argent des banques ,c’est ce que l’on appel utiliser un levier financier.
c’est sur que dans de rare cas les gens on l’argent pour financer leurs projets, je suis comme toi je pense qu’il faut utiliser ce levier.
à bientôt
Jérôme